Post-Midterm 2 Practice Problems
last updated on December 8th, 2025 at 2:30AM
This page contains several practice problems for content introduced after Midterm 2. They are sorted by topic:
- Problems 1-14 are on Eigenvalues and Eigenvectors.
- Problems 15-21 are on the Singular Value Decomposition.
- Problems 22-26 are on Principal Components Analysis.
The problems range in difficulty, and aren’t necessarily indicative of the difficulty or styles of problems you will see on the real exam; some problems are more open-ended than we’d ask on an exam, and are designed to encourage you to review parts of the course notes.
As we’re able to, we will embed videos to certain problems here. A few have already been embedded below.
Eigenvalues and Eigenvectors
Problem 1
Let
\[A = \begin{bmatrix} 3 & -1 & 1 \\ 0 & 5 & 4 \\ 0 & 0 & 5 \end{bmatrix}\]Find the eigenvalues and eigenvectors of \(A\). If \(A\) is diagonalizable, write it in the form \(A = V \Lambda V^{-1}\), and if it is not, explain why not.
Problem 2
Suppose \(A\) is a \(3 \times 3\) matrix such that the eigenspace for \(\lambda = 1\) is the line spanned by \(\begin{bmatrix} 1 \\ 2 \\ 2 \end{bmatrix}\), and the eigenspace for \(\lambda = -5\) is the plane \(2x - 3y + 4z = 0\).
- Why is \(A\) diagonalizable?
- Find matrices \(V\) and \(\Lambda\) such that \(A = V \Lambda V^{-1}\).
Problem 3
In each part, answer the following questions about the \(n \times n\) matrix \(A\):
- What is the value of \(n\)?
- Is \(A\) invertible?
- Is \(A\) diagonalizable, or is it impossible to tell?
\(A\) has characteristic polynomial \(p(\lambda) = \lambda^3 - 16\lambda\).
\(A\) has characteristic polynomial \(p(\lambda) = (2 - \lambda)(4 - \lambda)(5 - \lambda)^2\).
Problem 4
Suppose \(A\) is an \(n \times n\) matrix with characteristic polynomial \(p(\lambda) = \lambda^3 (2 - \lambda)(4 - \lambda)\).
Fill in the blank: \(A\) is diagonalizable if and only if \(\text{rank}(A) = \_\_\_\_\).
Problem 5
Suppose \(A\) is a \(2 \times 2\) matrix with characteristic polynomial \(p(\lambda)\), where \(p(0) = 0\) and \(p(1) = -5\).
Find two possible matrices \(A\).
Problem 6
Suppose \(A\) is a diagonalizable \(3 \times 3\) matrix with eigenvalue decomposition \(A = V \Lambda V^{-1}\).
Suppose \(\vec v_1\), \(\vec v_2\), and \(\vec v_3\) are the columns of \(V\), and suppose \(\vec x \in \mathbb{R}^3\) is some other vector such that
\[x = 3 \vec v_1 - 2 \vec v_2 + 4 \vec v_3, \qquad A \vec x = 15 \vec v_1 - 8 \vec v_3\]Why is it guaranteed that no other linear combination of \(\vec v_1\), \(\vec v_2\), and \(\vec v_3\) can equal \(\vec x\)?
Find \(V^{-1} \vec x\).
What are the eigenvalues of \(A\)?
Problem 7
Identify whether each of the following statements is true or false, and justify your answer.
- If \(A\) is upper triangular, then \(A\) is diagonalizable.
- Every \(13 \times 13\) matrix has at least one real eigenvalue.
- There exists a \(7 \times 7\) matrix with an eigenvalue \(\lambda\) with algebraic multiplicity \(\text{AM}(\lambda) = 3\) and geometric multiplicity \(\text{GM}(\lambda) = 4\).
- There exists a non-zero \(7 \times 7\) matrix with an eigenvalue of \(0\) with geometric multiplicity \(\text{GM}(0) = 7\).
- If two matrices have the same characteristic polynomial, then either they are both diagonalizable, or they are both not diagonalizable.
Problem 8
Suppose \(A\) and \(B\) are both \(2 \times 2\) matrices with an eigenvalue of \(5\).
- Is \(AB\) also guaranteed to have an eigenvalue of \(5\)?
- Is \(A + B\) also guaranteed to have an eigenvalue of \(5\)?
Problem 9
- Suppose \(A\) has an eigenvalue of \(\lambda\). Show that \(A^k\) has an eigenvalue of \(\lambda^k\) with the same eigenvector.
- The converse of the statement above is false — that is, just because \(A^k\) has an eigenvalue of \(\lambda^k\), it does not mean \(A\) has an eigenvalue of \(\lambda\). Find a counterexample, by finding a matrix \(A\) such that \(A^2\) has an eigenvalue of \(-1\) such that \(A\) has no real eigenvalues. Is \(A\) diagonalizable?
Problem 10
Let \(A = \begin{bmatrix} 1 & 3 \\ 3 & 1 \end{bmatrix}\).
- What is the name of the theorem that guarantees that \(A\) is diagonalizable?
- What does that theorem say about the eigenvectors of \(A\)?
Problem 11
Prove that if \(\vec u\) and \(\vec v\) are eigenvectors of the symmetric matrix \(S\) corresponding to different eigenvalues, then \(\vec u\) and \(\vec v\) are orthogonal. This is the essence of the spectral theorem.
Problem 12
Consider the symmetric matrix \(A = \begin{bmatrix} 4 & 1 & 1 \\ 1 & 4 & 1 \\ 1 & 1 & 4 \end{bmatrix}\). \(A\) can be diagonalized into \(A = V \Lambda V^{-1}\) as follows:
\[\underbrace{\begin{bmatrix} 4 & 1 & 1 \\ 1 & 4 & 1 \\ 1 & 1 & 4 \end{bmatrix}}_{A} = \underbrace{\begin{bmatrix} \dfrac{1}{\sqrt{3}} & \dfrac{2}{\sqrt{6}} & \dfrac{1}{\sqrt{6}} \\ \dfrac{1}{\sqrt{3}} & -\dfrac{1}{\sqrt{6}} & -\dfrac{2}{\sqrt{6}} \\ \dfrac{1}{\sqrt{3}} & -\dfrac{1}{\sqrt{6}} & \dfrac{1}{\sqrt{6}} \end{bmatrix}}_{V} \underbrace{\begin{bmatrix} 6 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{bmatrix}}_{\Lambda} \underbrace{\left( \begin{bmatrix} \dfrac{1}{\sqrt{3}} & \dfrac{2}{\sqrt{6}} & \dfrac{1}{\sqrt{6}} \\ \dfrac{1}{\sqrt{3}} & -\dfrac{1}{\sqrt{6}} & -\dfrac{2}{\sqrt{6}} \\ \dfrac{1}{\sqrt{3}} & -\dfrac{1}{\sqrt{6}} & \dfrac{1}{\sqrt{6}} \end{bmatrix} \right)^{-1}}_{V^{-1}}\]Note that \(V\) is not an orthogonal matrix.
- Why is the above statement not a contradiction of the spectral theorem?
- What is the name of the process that allows us to convert a collection of vectors into an orthonormal basis?
- Find matrices \(Q\) and \(\Lambda\) such that \(A = Q \Lambda Q^T\).
Problem 13
Recall, a symmetric matrix \(A\) is positive semidefinite if \(\vec v^T A \vec v \geq 0\) for all \(\vec v \in \mathbb{R}^n\).
- Are all positive semidefinite matrices invertible?
- Are all positive semidefinite matrices diagonalizable?
- If we change positive semidefinite to positive definite, how do the answers to the previous statements change?
- Fill in the blanks: A symmetric matrix \(A\) is positive semidefinite if and only if all of its eigenvalues are ____.
- Draw a Venn diagram of the relationship between the following sets of square matrices: positive semidefinite, positive definite, symmetric, diagonalizable, and invertible.
Problem 14
Consider the function
\[f(x, y) = \frac{8xy + 15y^2}{x^2 + y^2}\]visualized here on Desmos.
The goal of this problem is to find the minimum and maximum values of \(f(x, y)\), without taking any partial derivatives. You might want to review this section of Chapter 5.4.
- Write the numerator of \(f(x, y)\) as a quadratic form, \(\vec x^T A \vec x\), where \(\vec x = \begin{bmatrix} x \\ y \end{bmatrix}\) and \(A\) is a \(2 \times 2\) matrix.
- Using the quadratic form, find the minimum and maximum values of \(f(x, y)\).
- There are infinitely many points that minimize \(f(x, y)\) and infinitely many points that maximize \(f(x, y)\). Where do these points lie?
Singular Value Decomposition
Note: None of these questions are of the form “find the singular value decomposition of a matrix”; you can find problems like those in Chapter 5.3 and in Homework 11. Make sure to practice those too.
Problem 15
Suppose the matrix \(X\) has the singular value decomposition \(X = U \Sigma V^T\) where
\[U = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}, \quad \Sigma = \begin{bmatrix} \sigma_1 & 0 & 0 \\ 0 & 2 & 0 \end{bmatrix}, \quad V = \begin{bmatrix} 1/\sqrt{2} & | & 0 \\ 0 & \vec v_2 & 1 \\ 1/\sqrt{2} & | & 0 \end{bmatrix}\]- How many rows and columns does \(X\) have? What is \(\text{rank}(X)\)?
- Find \(\vec v_2\).
- Given that the first column of \(X\) and third column of \(X\) sum to \(\begin{bmatrix} 0 \\ 5 \end{bmatrix}\), find \(\sigma_1\). Hint: Recall that \(X \vec v_i = \sigma_i \vec u_i\) for \(i = 1, 2, ..., \text{rank}(X)\).
Problem 16
Consider the rank-\(2\) matrix \(X = \begin{bmatrix} 1 & 2 & 2 \\ 1 & 3 & 3 \end{bmatrix}\).
- Write \(X\) as a sum of two rank-1 outer products, e.g. \(X = \vec x_1 \vec y_1^T + \vec x_2 \vec y_2^T\).
- Find \(X X^T\) and \(X^T X\), and the trace and determinant of each.
- If \(X\) is any \(n \times d\) matrix, which of the following are guaranteed to be true, and why?
Problem 17
Suppose \(X\) is a symmetric \(n \times n\) matrix with singular value decomposition \(X = U \Sigma V^T\). (Note that we are assuming \(X\) is square, which isn’t typically the case for the singular value decomposition.)
Show that the diagonal entries of \(\Sigma\) are the absolute values of the eigenvalues of \(X\), i.e. \(\sigma_i = \mid \lambda_i \mid\) for all \(i = 1, 2, ..., \text{rank}(X)\).
Problem 18
To find the singular values of \(X\), we take the square roots of the non-zero eigenvalues of \(X^TX\) (which are the same as the non-zero eigenvalues of \(XX^T\)).
\[\sigma_i = \sqrt{\lambda_i}\]Why is it guaranteed that the eigenvalues of \(X^TX\) are non-negative? (Hint: What does this have to do with Problem 13?)
Problem 19
Consider the matrix \(X\) whose singular value decomposition is given by
\[X = \underbrace{\begin{bmatrix} 1/2 & 1/2 & 1/2 & 1/2 \\ 1/2 & 1/2 & -1/2 & -1/2 \\ 1/2 & -1/2 & 1/2 & -1/2 \\ 1/2 & -1/2 & -1/2 & 1/2 \end{bmatrix}}_{U} \underbrace{\begin{bmatrix} 8 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 1 \end{bmatrix}}_{\Sigma} \underbrace{\begin{bmatrix} \sqrt{2}/2 & \sqrt{2}/2 & 0 \\ -\sqrt{2}/2 & \sqrt{2}/2 & 0 \\ 0 & 0 & 1 \end{bmatrix}}_{V^T}\]- Find the best rank-1 approximation of \(X\).
- Let \(X_1\) be the matrix you found in the previous part. In Homework 11, Problem 2, you were introduced to the Frobenius norm of a matrix, which can be thought of as the length of the norm of the matrix, if you think of it as one long \(n \times d\) vector. Explain why the Frobenius norm of \(X - X_1\) is equal to \(\sqrt{3^2 + 1^2} = \sqrt{10}\).
- Find the best rank-2 approximation of \(X\). There’s no need to work out the entire calculation, but make sure you know how to do it.
Problem 20
Suppose \(X\) is a \(5 \times 2\) matrix with singular value decomposition \(X = U \Sigma V^T\).
Suppose \(\vec v_1\) and \(\vec v_2\) are the first and second columns of \(V\), respectively. Furthermore, suppose \(\vec w \in \mathbb{R}^2\) is a vector such that
\[\vec w = 3 \vec v_1 - \vec v_2\]- Find \(V^T \vec w\).
- Suppose \(X\)’s two singular values are \(\sigma_1 = 10\) and \(\sigma_2 = 3\). Find \(\Sigma V^T \vec w\).
- Let \(\vec z = \Sigma V^T \vec w\). In English, what does \(\vec z\) represent, relative to \(\vec w\)?
Problem 21
Let \(X = U \Sigma V^T\) be singular value decomposition of some \(n \times d\) matrix \(X\), and let \(P = U \Sigma\). Suppose we compute the singular value decomposition of \(P\) into
\[P = U_P \Sigma_P V_P^T\]What is \(V_P^T\)? Justify your answer conceptually, not just algebraically. Hint: What is \(P^TP\) in terms of \(U\) and \(\Sigma\)?
Principal Components Analysis
Problem 22
In Homework 11, Problem 4 (and in Chapter 5.4), we plotted a 2-dimensional representation of a higher-dimensional dataset. Let \(\tilde X\) be the mean-centered version of the dataset.
Fill in the blanks: to create this plot, we plotted the first 2 (1) of (2).
- rows / columns
- \[\tilde X \qquad U \qquad V \qquad V^T \qquad U \Sigma \qquad \Sigma V^T \qquad \tilde X V \qquad U \Sigma V^T\]
(there may be more than one correct answer; identify all of them)
Problem 23
Suppose \(\tilde X\) is a mean-centered \(n \times d\) matrix, and let \(\tilde X = U \Sigma V^T\) be the singular value decomposition of \(\tilde X\).
All you are given is that \(\Sigma = \begin{bmatrix} 10 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 0.1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}\).
- How many rows and columns does \(\tilde X\) have? What is \(\text{rank}(\tilde X)\)?
- What is the variance of the second principal component?
- What is the proportion of the total variance in \(\tilde X\) that is accounted for by the first principal component? The second? The first and second together?
Problem 24
Suppose \(X\) is a \(51 \times 5\) matrix, whose first 3 rows are given by
\[\text{first 3 rows of } X = \begin{bmatrix} 3 & 12 & 5 & 1 & 5 \\ 3 & 4 & 8 & 2 & 1 \\ 1 & 2 & 7 & 2 & 1 \end{bmatrix}\]Consider the following information about the columns of \(X\).
| Column 1 | Column 2 | Column 3 | Column 4 | Column 5 | |
|---|---|---|---|---|---|
| Mean | 2 | 3 | 10 | 5 | 1 |
| Variance | 0.3 | 0.3 | _ | 0.3 | 0.3 |
Let \(\tilde X\) be the mean-centered version of \(X\), and let \(\tilde X = U \Sigma V^T\) be the singular value decomposition of \(\tilde X\).
Suppose the values along the diagonal of \(\Sigma\) are \(9\), \(4\), \(2\), \(1\), and \(0\).
- What is \(\text{rank}(\tilde X)\)? (Note that in general, unlike I accidentally said in Thursday’s lecture, \(\text{rank}(\tilde X)\) is not necessarily equal to \(\text{rank}(X)\): it is possible for \(\text{rank}(\tilde X)\) to equal \(\text{rank}(X) - 1\). Think about why this is the case!)
- We want to choose the first \(k\) principal components, such that at least \(95\%\) of the variance in \(X\) is accounted for. What is the smallest possible value of \(k\) that we can choose?
- Notice that the table provided does not include the variance of column \(3\). Given all the information above, what is the variance of column \(3\)?
- Suppose \(\vec v_3 = \begin{bmatrix} 4/5 \\ 3/5 \\ 0 \\ 0 \\ 0 \end{bmatrix}\) is the third column of \(V\). What is the first entry of \(\vec u_3\), the third column of \(U\)? Hint: Remember that \(U \Sigma V^T\) is the singular value decomposition of \(\tilde X\), not \(X\).
- Prove that the entries of \(\tilde X \vec w\) sum to 0, for any \(\vec w \in \mathbb{R}^5\).
- Which of these four plots visualizes principal component 2 vs. principal component 1?
Problem 25
Let \(X\) be a \(20 \times 3\) matrix, let \(\tilde X\) be the centered version of \(X\), and let \(\tilde X = U \Sigma V^T\) be the singular value decomposition of \(\tilde X\).
Suppose the variances of the 3 columns of \(\tilde X\) are \(125\), \(20\), and \(5\), respectively. What is the smallest possible value of \(\sigma_1\), the largest singular value of \(\tilde X\)?
Problem 26
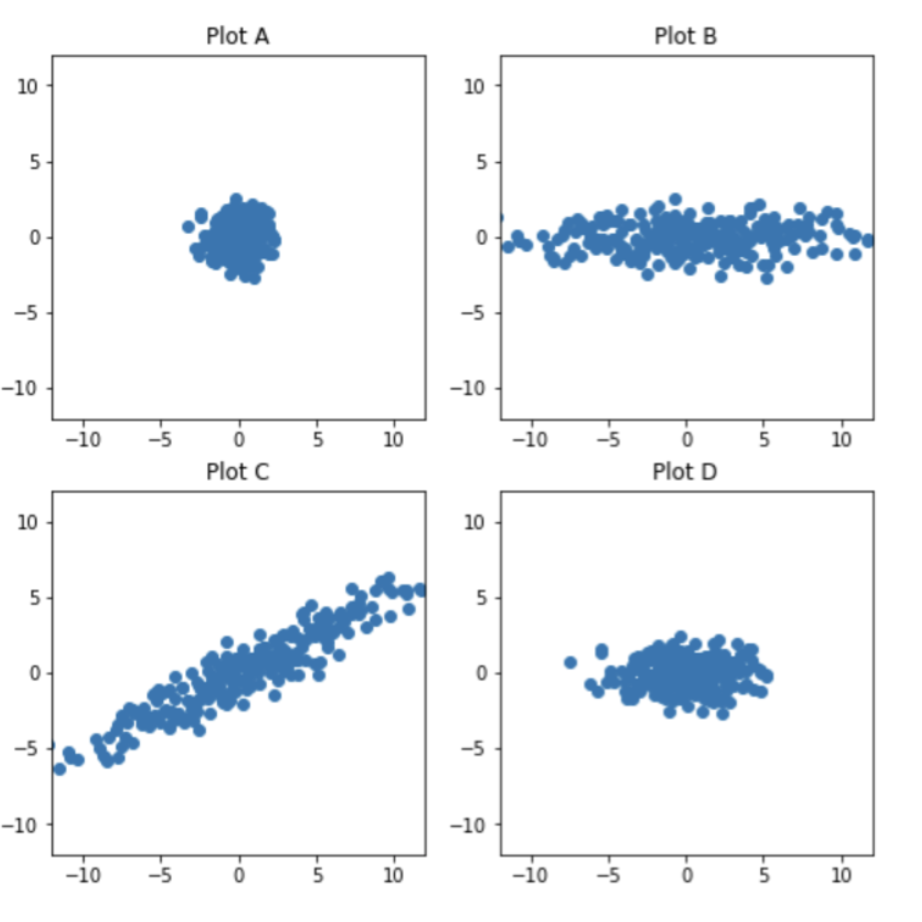
Suppose \(A\), \(B\), and \(C\) are each \(100 \times 2\) matrices, representing \(n = 100\) points in \(\mathbb{R}^2\). The three datasets are shown in the scatter plots below. (Matrix \(A\) is in Plot A, matrix \(B\) is in Plot B, and matrix \(C\) is in Plot C.)

Assume that \(A\), \(B\), and \(C\) are each already centered.
- If we applied PCA to each of the above datasets, and created just one principal component in each case, for which dataset would the first principal component have the smallest mean squared orthogonal error – \(A\), \(B\), or \(C\)?
Suppose \(\tilde X = U \Sigma V^T\) is the singular value decomposition of \(\tilde X\), and that \(\Sigma \approx \begin{bmatrix} 16 & 0 \\ 0 & 4 \\ 0 & 0 \\ \vdots & \vdots \\ 0 & 0\end{bmatrix}, \qquad \underbrace{V = \begin{bmatrix} 2/\sqrt{5} & 1/\sqrt{5} \\ -1/\sqrt{5} & 2/\sqrt{5} \end{bmatrix}}_{\textbf{not } V^T}\)
Which dataset is most likely to be \(\tilde X\) – \(A\), \(B\), or \(C\)?
- Suppose that in the graph of principal component 2 vs. principal component 1 (i.e. with PC 1 on the \(x\)-axis and PC 2 on the \(y\)-axis), a particular data point is plotted at \((4, 2)\). What is the corresponding point in the original (mean-centered) dataset? Your answer should be a tuple of two numbers, \((a, b)\) (or equivalently, a vector in \(\mathbb{R}^2\)).
Some problems were borrowed from this site.